How Do You Solve −log(x) = 5.4? | Socratic
You can put this solution on YOUR website! log((5+x)/(x-3)) = log 5,, 5+x = 5(x-3), 5+x = 5x - 15, 20 = 4x, x = 5. This value satisfies the original equation, and so is the final answer.Simple and best practice solution for log (x+5)=log (5x) equation. Check how easy it is, and learn it for the future. Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework. If it's not what You are looking for type in the equation solver your own equation and let us solve it.The base of the log is the same as the base of the expoenential form and in our case the base is 10. Identifying the exponent. The value of the exponent is what the log is equal too and in our case it is 5. Rewrite in exponential form. We already know the base is 10 and we want to raise it to the exponent of 5 so we get x=10 5. x=100000 Theorylog(x) = 5 log (x) = 5 Rewrite log(x) = 5 log (x) = 5 in exponential form using the definition of a logarithm. If x x and b b are positive real numbers and b b ≠ ≠ 1 1, then logb (x) = y log b (x) = y is equivalent to by = x b y = x. 105 = x 10 5 = xThe sum of logarithm of x to base 5 and logarithm of 5 to base x is equal to quotient of 5 by 2. This logarithmic equation helps us to find the value of x. It can be solved in mathematics by using logarithmic system. Step: 1
log(x+5)=log(5x) - solution
The calculator can also make logarithmic expansions of formula of the form `ln(a^b)` by giving the results in exact form : thus to expand `ln(x^3)`, enter expand_log(`ln(x^3)`), after calculation, the result is returned. The calculator makes it possible to obtain the logarithmic expansion of an expression.Find the domain of the function f(x) = log7(log5(log3(log2(2x^3 + 5x^2 - 14x)))) asked Oct 31, 2019 in Sets, relations and functions by Raghab ( 50.4k points) functionln(x) = log e (x) When e constant is the number: or . See: Natural logarithm. Inverse logarithm calculation. The inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: x = log-1 (y) = b y. Logarithmic function. The logarithmic function has the basic form of: f (x) = log b (x) Logarithm rulesThe logarithm log b (x) = y is read as log base b of x is equals to y. Please note that the base of log number b must be greater than 0 and must not be equal to 1. And the number (x) which we are calculating log base of (b) must be a positive real number. For example log 2 of 8 is equal to 3. log 2 (8) = 3 (log base 2 of 8) The exponential is 2
Solve Logarithmic form to exponential form log10x=5 Tiger
log 3 (x + 5) + 6 - 6 = 10 - 6; log 3 (x + 5) = 4 2. Rewrite the equation in exponential form. Using what you now know about the relationship between logarithms and exponential equations, break the logarithm apart and rewrite the equation in a simpler, solvable exponential form. Example:log 3 (x + 5) = 4 Comparing this equation to thex = [- 24 ± 29.5] / 10. x = [- 24 + 29.5] / 10 (or) x = [- 24 - 29.5] / 10. x = 0.55 (or) x = - 5.35. But by the definition of ln (log), 5x - 1 , x + 5 must be positive. Hence, x > 1/5, x > -5. Therefore, x must be greater than 1/5 and the solution -5.35 is invalid. The only solution is x = 0.55. Solution of the equation is x = 0.55.Log 5 is a formula invented by Bill James to estimate the probability that team A will win a game, based on the true winning percentage of Team A and Team B. It is equivalent to the Bradley-Terry_model used for paired comparisons, the Elo rating system used in chess, and the Rasch model used in the analysis of categorical data.Simple and best practice solution for log (x)+log (x-5)=log (36) equation. Check how easy it is, and learn it for the future. Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework. If it's not what You are looking for type in the equation solver your own equation and let us solve it.The solution is \displaystyle{x}=\frac{{2}}{{\log{{\left({5}\right)}}}} Explanation: A property of lohgarithms states that \displaystyle{\log{{\left({a}^{{b}}\right
Log calculator finds the logarithm function result (can be called exponent) from the given base number and a real number.
Logarithm
Logarithm is considered to be one of the basic concepts in mathematics. There are plenty of definitions, starting from really complicated and ending up with rather simple ones. In order to answer a question, what a logarithm is, let's take a look at the table below:
212223242526 248163264This is the table in which we can see the values of two squared, two cubed, and so on. This is an operation in mathematics, known as exponentiation. If we look at the numbers at the bottom line, we can try to find the power value to which 2 must be raised to get this number. For example, to get 16, it is necessary to raise two to the fourth power. And to get a 64, you need to raise two to the sixth power.
Therefore, logarithm is the exponent to which it is necessary to raise a fixed number (which is called the base), to get the number y. In other words, a logarithm can be represented as the following:
logb x = y
with b being the base, x being a real number, and y being an exponent.
For example, 23 = 8 ⇒ log2 8 = 3 (the logarithm of 8 to base 2 is equal to 3, because 23 = 8).Similarly, log2 64 = 6, because 26 = 64.
Therefore, it is obvious that logarithm operation is an inverse one to exponentiation.
212223242526 248163264log22 = 1 log24 = 2 log28 = 3 log216 = 4 log232 = 5 log264 = 6Unfortunately, not all logarithms can be calculated that easily. For example, finding log2 5 is hardly possible by just using our simple calculation abilities. After using logarithm calculator, we can find out that
log2 5 = 2,32192809
There are a few specific types of logarithms. For example, the logarithm to base 2 is known as the binary logarithm, and it is widely used in computer science and programming languages. The logarithm to base 10 is usually referred to as the common logarithm, and it has a huge number of applications in engineering, scientific research, technology, etc. Finally, so called natural logarithm uses the number e (which is approximately equal to 2.71828) as its base, and this kind of logarithm has a great importance in mathematics, physics, and other precise sciences.
The logarithm logb(x) = y is read as log base b of x is equals to y.Please note that the base of log number b must be greater than 0 and must not be equal to 1. And the number (x) which we are calculating log base of (b) must be a positive real number.
For example log 2 of 8 is equal to 3.
log2(8) = 3 (log base 2 of 8) The exponential is 23 = 8 Common Values for Log Base Logarithmic IdentitiesList of logarithmic identites, formulas and log examples in logarithm form.
Logarithm of a Product logb(x·y) = logb(x) + logb(y) log2(5·7) = log2(5) + log2(7) Logarithm of a Quotient logb(x/y) = logb(x) - logb(y) log2(5/7) = log2(5) - log2(7) Logarithm of a Power logb(xy) = y·logb(x) log2(57) = 7·log2(5) Change of Base logb(x) = (logk(x)) / (logk(b)) Natural Logarithm Examples ln(2) = loge(2) = 0.6931 ln(3) = loge(3) = 1.0986 ln(4) = loge(4) = 1.3862 ln(5) = loge(5) = 1.609 ln(6) = loge(6) = 1.7917 ln(10) = loge(10) = 2.3025 Logarithm Values TablesList of log function values tables in common base numbers.
log2(x)NotationValuelog2(1)lb(1)0log2(2)lb(2)1log2(3)lb(3)1.584963log2(4)lb(4)2log2(5)lb(5)2.321928log2(6)lb(6)2.584963log2(7)lb(7)2.807355log2(8)lb(8)3log2(9)lb(9)3.169925log2(10)lb(10)3.321928log2(11)lb(11)3.459432log2(12)lb(12)3.584963log2(13)lb(13)3.70044log2(14)lb(14)3.807355log2(15)lb(15)3.906891log2(16)lb(16)4log2(17)lb(17)4.087463log2(18)lb(18)4.169925log2(19)lb(19)4.247928log2(20)lb(20)4.321928log2(21)lb(21)4.392317log2(22)lb(22)4.459432log2(23)lb(23)4.523562log2(24)lb(24)4.584963 log10(x)NotationValuelog10(1)log(1)0log10(2)log(2)0.30103log10(3)log(3)0.477121log10(4)log(4)0.60206log10(5)log(5)0.69897log10(6)log(6)0.778151log10(7)log(7)0.845098log10(8)log(8)0.90309log10(9)log(9)0.954243log10(10)log(10)1log10(11)log(11)1.041393log10(12)log(12)1.079181log10(13)log(13)1.113943log10(14)log(14)1.146128log10(15)log(15)1.176091log10(16)log(16)1.20412log10(17)log(17)1.230449log10(18)log(18)1.255273log10(19)log(19)1.278754log10(20)log(20)1.30103log10(21)log(21)1.322219log10(22)log(22)1.342423log10(23)log(23)1.361728log10(24)log(24)1.380211 loge(x)NotationValueloge(1)ln(1)0loge(2)ln(2)0.693147loge(3)ln(3)1.098612loge(4)ln(4)1.386294loge(5)ln(5)1.609438loge(6)ln(6)1.791759loge(7)ln(7)1.94591loge(8)ln(8)2.079442loge(9)ln(9)2.197225loge(10)ln(10)2.302585loge(11)ln(11)2.397895loge(12)ln(12)2.484907loge(13)ln(13)2.564949loge(14)ln(14)2.639057loge(15)ln(15)2.70805loge(16)ln(16)2.772589loge(17)ln(17)2.833213loge(18)ln(18)2.890372loge(19)ln(19)2.944439loge(20)ln(20)2.995732loge(21)ln(21)3.044522loge(22)ln(22)3.091042loge(23)ln(23)3.135494loge(24)ln(24)3.178054 Related Log Base CalculatorsPLEASE HELP!!!! Solve logx + 5 36 = 2. options: x=1 x=11 x ...
Решить неравенство log_{x+1}(log_{2}(4^x-4*2^x+5))
Which equation represents the transformed function below ...

Integrale indefinito con logaritmo

Logarithmic and exponential functions - Topics in precalculus

Tarea:Investigacion Las Comunicaciones
Logarithmic Functions

2x X X - SEONegativo.com

no.15) himpunan penyelesaian persamaan: 6 log (x-3) + 6 ...
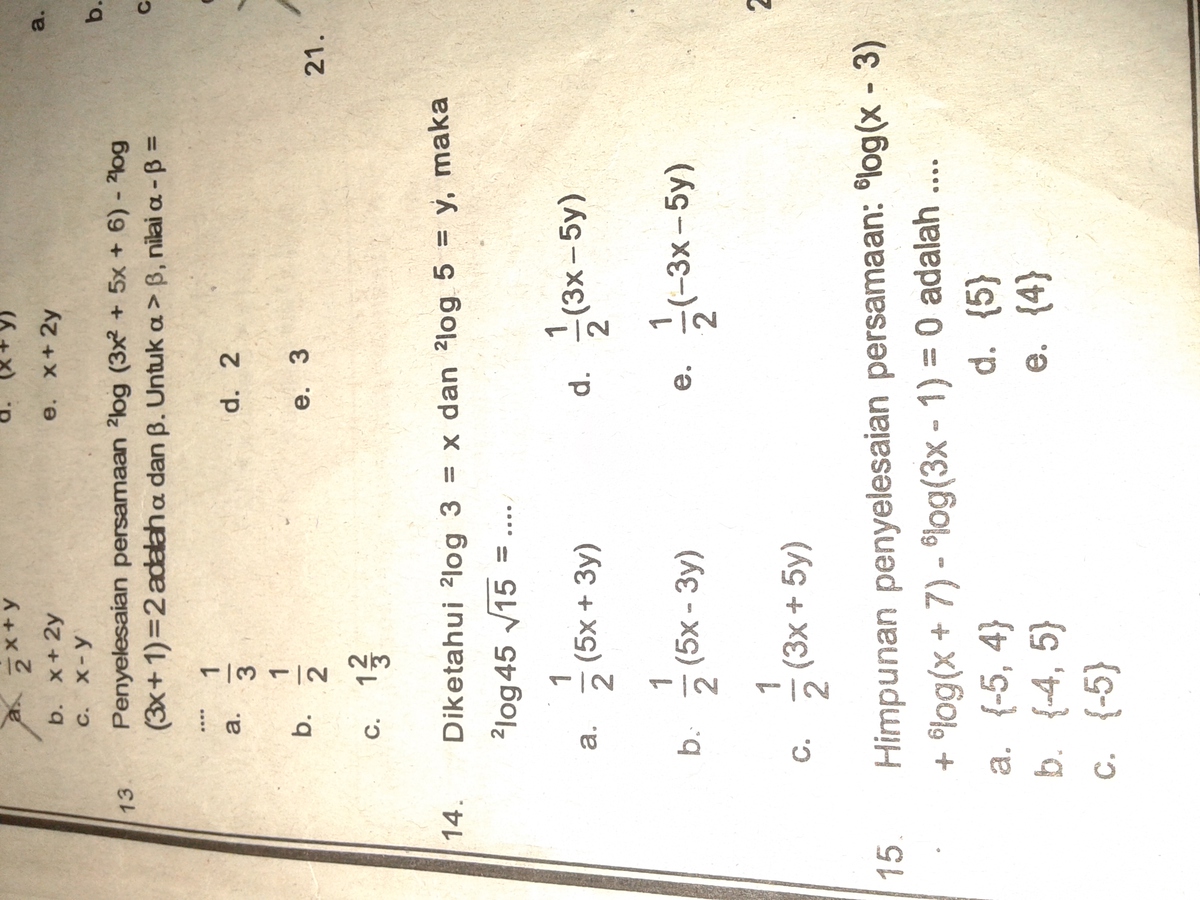
log 11-x (x+7)*log x+5 (9-x) ≤0 Очень подробно, если можно ...

Математика Решите неравенство: log(11-x) (x+7) log(x+5) (9 ...

If log5 + log(5x+1) = log(x+5) + 1, then x is equal to ...
Решите неравенство log(5-x)(x+5)*log(x+4)(4-x) меньше или ...

Pembahasan SBMPTN 2014 Matematika IPA Kode 591 - CATATAN ...

Situação 3 da função logarítmica

Logarithmic Equations - examples of problems with solutions

Solved: Express X/x - 3 - 18/x^2 - 9 In The Lowest Term A ...
スクリーンショット 2020-02-02 20.35.56|とものブログ

4.4E: Exercises - Graphs of Logarithmic Functions ...

Решите неравенство log(x+5)(27-27x+9x^2-x^3) ≥ 0

log 11-x (x+7)*log x+5 (9-x) ≤0 Очень подробно, если можно ...


Aucun commentaire:
Enregistrer un commentaire
Remarque : Seul un membre de ce blog est autorisé à enregistrer un commentaire.